Российское геометрическое ядро RGK - Построение поверхностей и задачи сглаживания(часть 2)

Продолжение публикации.

Сергей Козлов и Леонид Баранов представляют геометрическое ядро RGK

При построении поверхностей в ядре особое внимание уделяется их качеству — как с точки зрения соблюдения требований точности построения, так и в плане минимизации количества управляющих точек и регуляризации параметризации. Поскольку разработчики RGK имеют прямой доступ к функциональности, пожалуй, лучшего твердотельного ядра в мире — Parasolid, это позволяет проводить непредвзятые исследования и сравнение результатов. В настоящее время качество алгоритмов генерации поверхностей в RGK в целом сопоставимо с этим ядром и продолжает постоянно совершенствоваться, так как текущей задачей разработчиков является достижение функционального паритета с лучшими мировыми ядрами. В связи с этим в процессе разработки проводится большая исследовательская работа по анализу качества алгоритмов по сравнению и с другими конкурирующими решениями «тяжёлого» класса.

Как известно, одним из наиболее сложных как в математическом, так и алгоритмическом отношении классом задач геометрического моделирования являются задачи сглаживания (скругления) поверхностей. Учитывая это, при разработке ядра RGK особое внимание уделяется именно данной функциональности.

В настоящее время в сглаживании рёбер поддерживаются практически все основные режимы управления формой, известные по функциональности так называемых систем «тяжёлого» класса: сечение постоянного и переменного радиуса; заданная ширина, как в постоянном, так и переменном режимах; переменные сечения с кривыми второго порядка (эллипсы, параболы, гиперболы); режимы гладких переходов и сохранения рёбер на всех типах сглаживаний; сохранение кривизны — G2 гладкость (рис. 4); задание отступов от вершины при вершинном сглаживании.

Задание граничных условий в генераторе по сечениям

Рис. 4. Задание граничных условий в генераторе «по сечениям»: G2-гладкое сопряжение поверхностей

Особенно стоит отметить архитектуру алгоритма, которая позволяет в едином формализме поддерживать сглаживание как рёбер, так и граней, а также трёхгранное сглаживание, тем самым обеспечивая очень высокую гибкость алгоритма и возможность развития. Большая работа проделана в части топологической робастности алгоритма сглаживания. Например, в зависимости от заданного радиуса алгоритм умеет делать большие перестройки топологии тела (рис. 5, 6).

Алгоритм не цепляется за родительские ребра

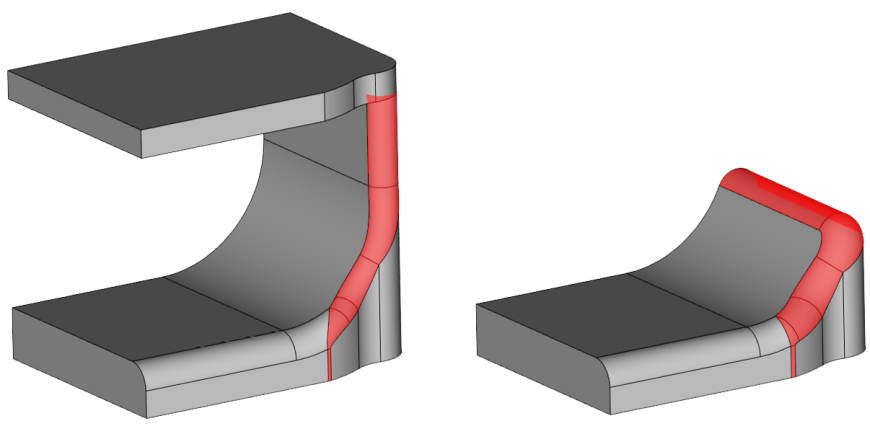Рис. 5. Алгоритм «не цепляется» за родительские ребра — его поведение определяется радиусом

Выход алгоритма сглаживания на соседние грани при большом радиусе поверхности

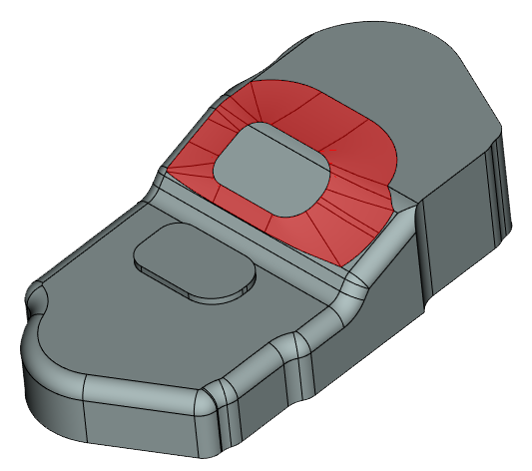Рис. 6. Выход алгоритма сглаживания на соседние грани при большом радиусе поверхности (режим сохранения ребра)

Является допустимым построение сглаживания большего радиуса по меньшему. Такая задача возникает довольно часто при практическом моделировании (рис. 7).

Обработка участков с радиусом кривизны, меньшим, чем текущий радиус сглаживания

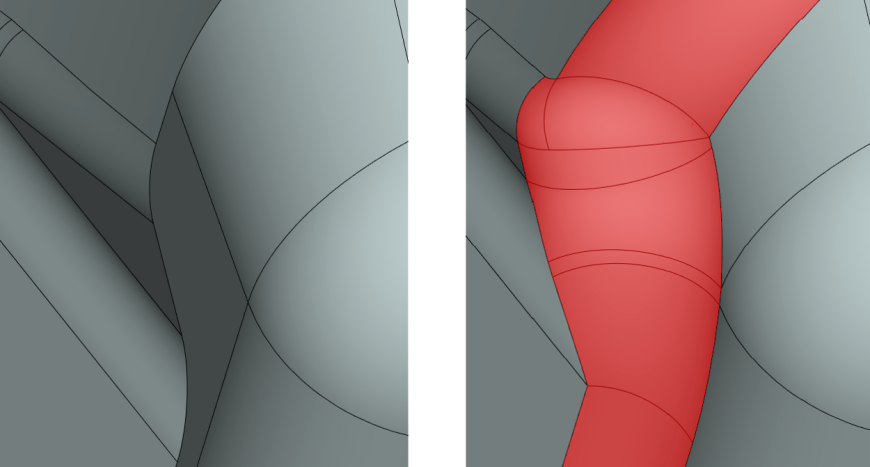Рис.7. Обработка участков с радиусом кривизны, меньшим, чем текущий радиус сглаживания

Поддерживаются различные «переполнения», то есть переходы на гладкие соседние грани, а также, при необходимости, сохранение рёбер (рис. 8-10).

Поддержка различных сценариев при выходе на гладкие рёбра

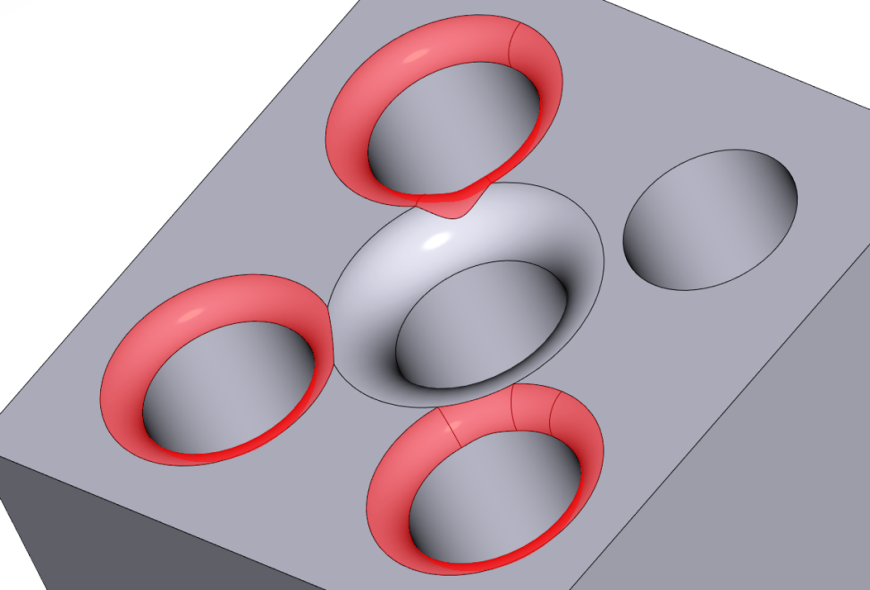Рис. 8. Поддержка различных сценариев при выходе на гладкие рёбра

Сохранение ребра при работе с большими радиусами сглаживания

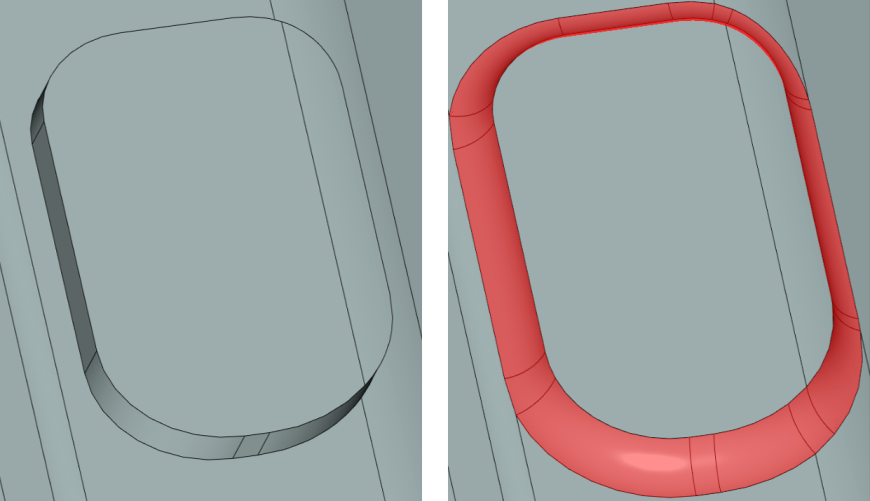Рис. 9. Сохранение ребра при работе с большими радиусами сглаживания

Режим сохранения острых рёбер на переменном сглаживании

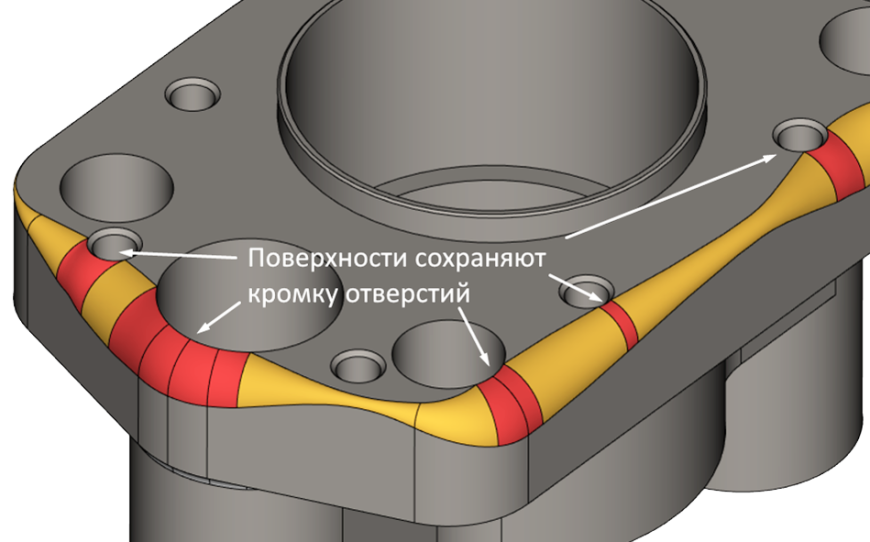Рис. 10. Режим сохранения острых рёбер на переменном сглаживании (обеспечивается G1 гладкость всей последовательности граней)

Особого внимания заслуживает способность алгоритма сглаживания RGK обрабатывать вырождение топологических элементов (рис. 11).

Обработка исчезновения граней в предельном случае

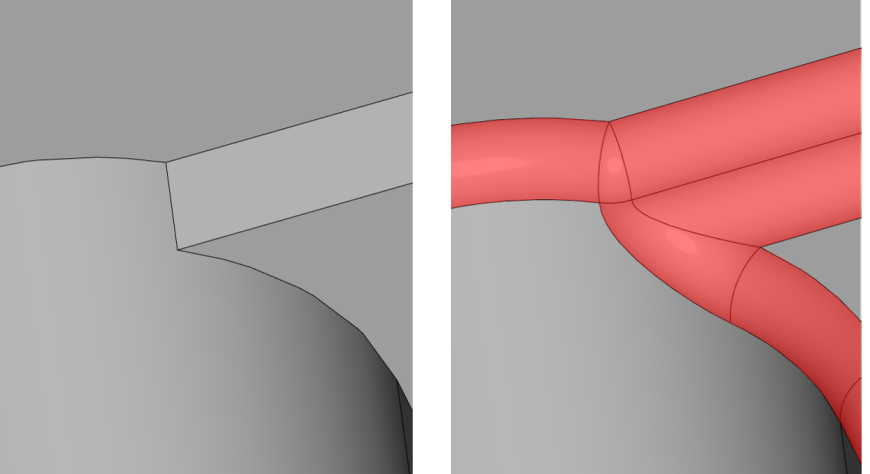Рис. 11. Обработка исчезновения граней в предельном случае

Поддерживается сложная топология перекрытий сглаживаний, что значительно повышает качество работы алгоритма при реальном применении (рис. 12).

Пример поддержки перекрытия сглаживаний из нескольких граней

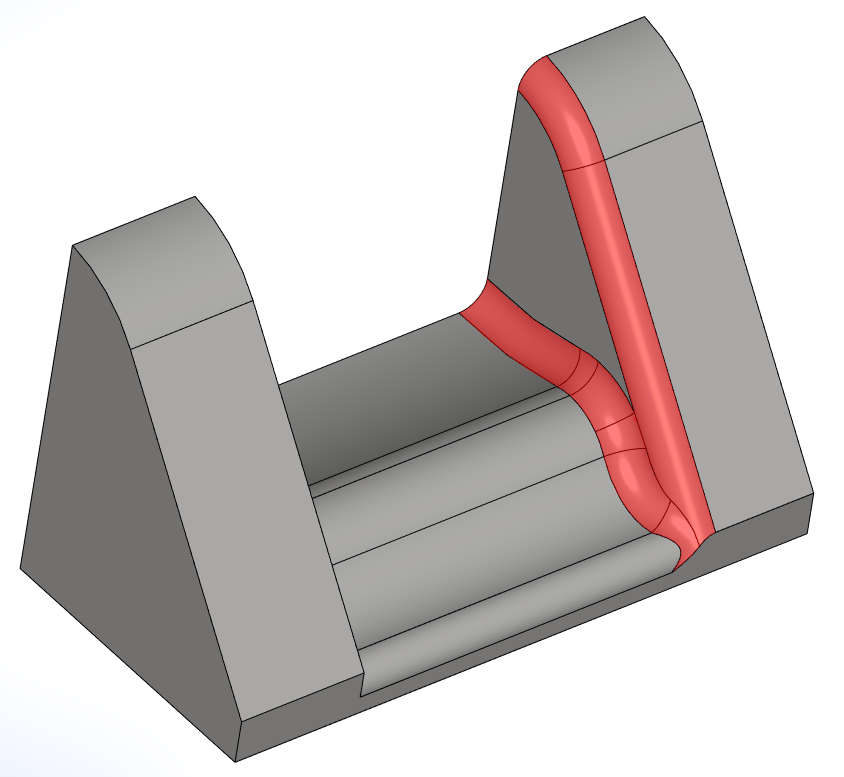Рис. 12. Пример поддержки перекрытия сглаживаний из нескольких граней

Интересные результаты достигнуты при построении переменного сглаживания. В частности, поддерживается обработка перекрытия сглаживающих последовательностей с перевычислением закона изменения радиуса в области перекрытия (рис. 13).

Выпукло-вогнутое сглаживание переменным радиусом

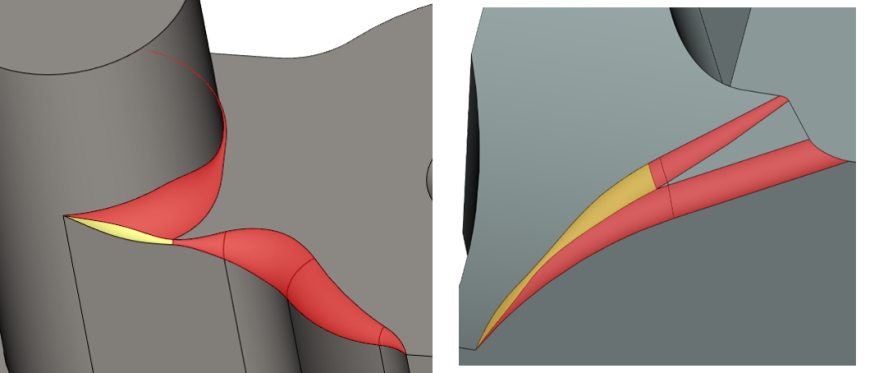Рис. 13. Выпукло-вогнутое сглаживание переменным радиусом

Естественно, алгоритмами RGK реализована поддержка различных сечений переменного радиуса (рис. 14).

Использование переменных законов смещения при рёберном сглаживании в RGK

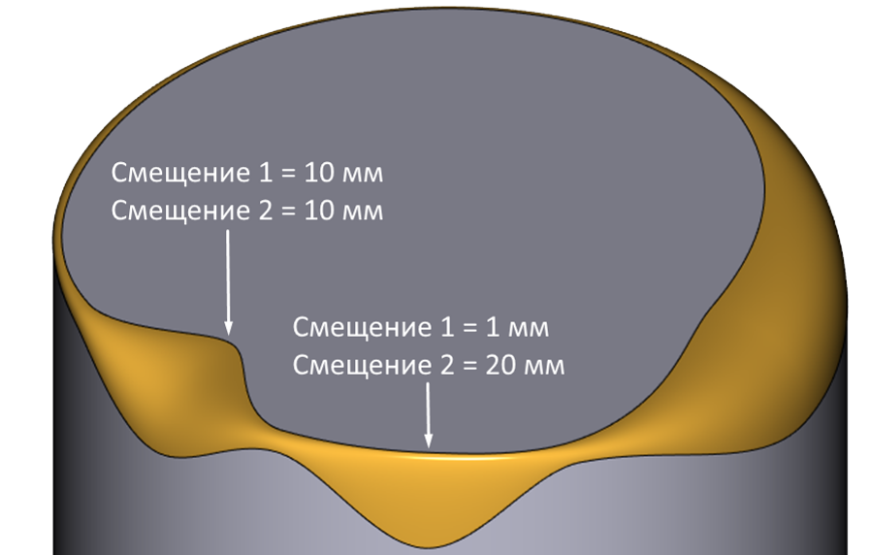Рис. 14. Использование переменных законов смещения при рёберном сглаживании в RGK

Использование управления типом кривой сечения через выпуклость-дискриминант конического сечения

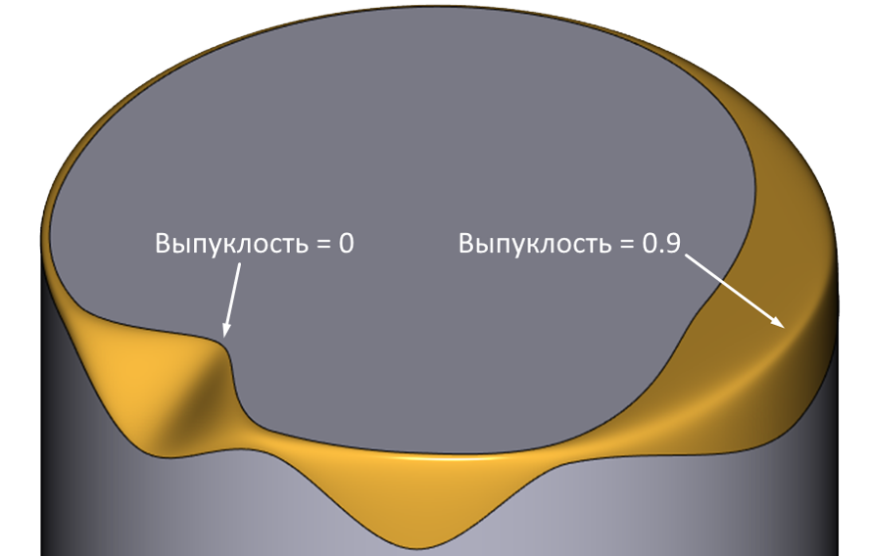Рис. 15. Использование управления типом кривой сечения через выпуклость-дискриминант конического сечения (переход от отрезка прямой к гиперболе)

Поддержка G2 гладкости на переменном и постоянном радиусах

Рис. 16. Поддержка G2 гладкости на переменном и постоянном радиусах

Поддержка режима постоянной ширины сечения для разных типов сечения

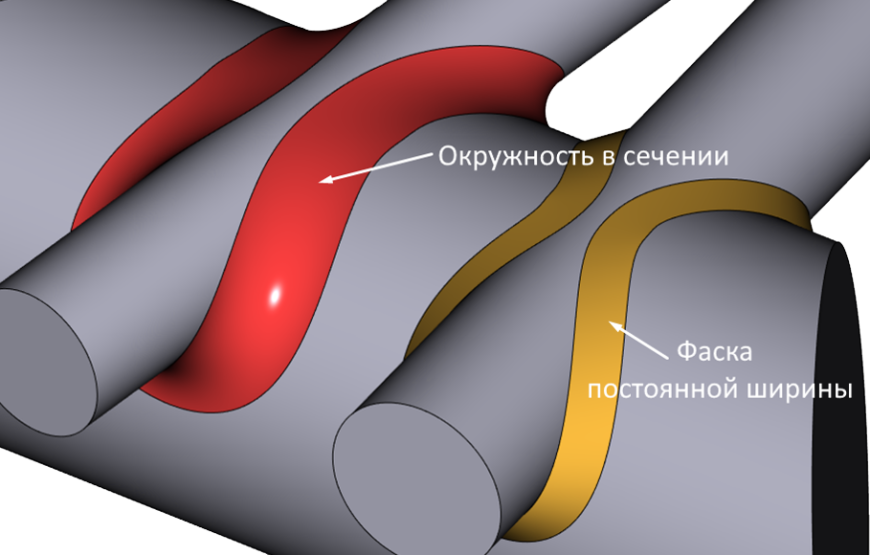Рис. 17. Поддержка режима постоянной ширины сечения для разных типов сечения

Пример работы режима заданной ширины

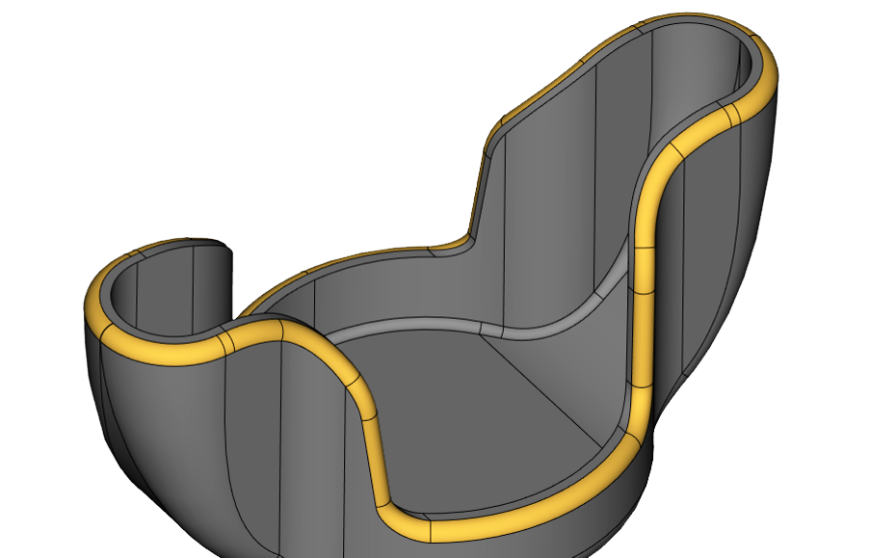Рис. 18. Пример работы режима заданной ширины

Кроме того, разработана математика построения гладких «затягиваний» n-угольных областей (рис. 19).

G1 затягивание n-угольных областей

Рис. 19. G1 затягивание n-угольных областей

Эти разработки позволяют, в частности, решать задачу построения поверхностей с отступами от вершины (setback) — рис. 20 и 21.

Применение алгоритма затягивания области для задачи отступов

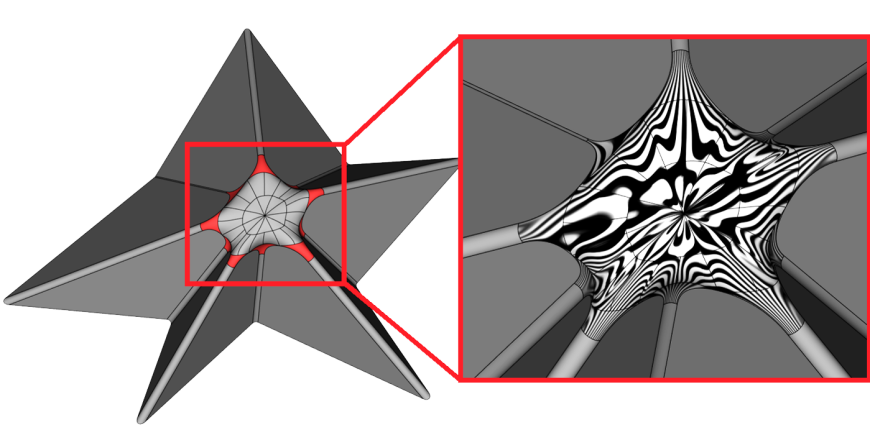Рис. 20. Применение алгоритма затягивания области для задачи отступов

Наглядный пример задачи отступов

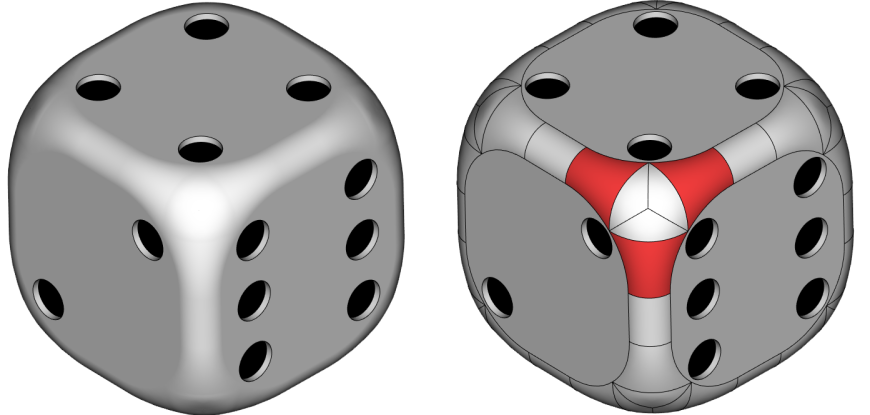Рис. 21. Наглядный пример задачи отступов

Алгоритм сглаживания работает как на твёрдых, так и на поверхностных телах — в RGK нет различий между этими топологиями (рис. 22).

Сглаживание ребра поверхностного тела

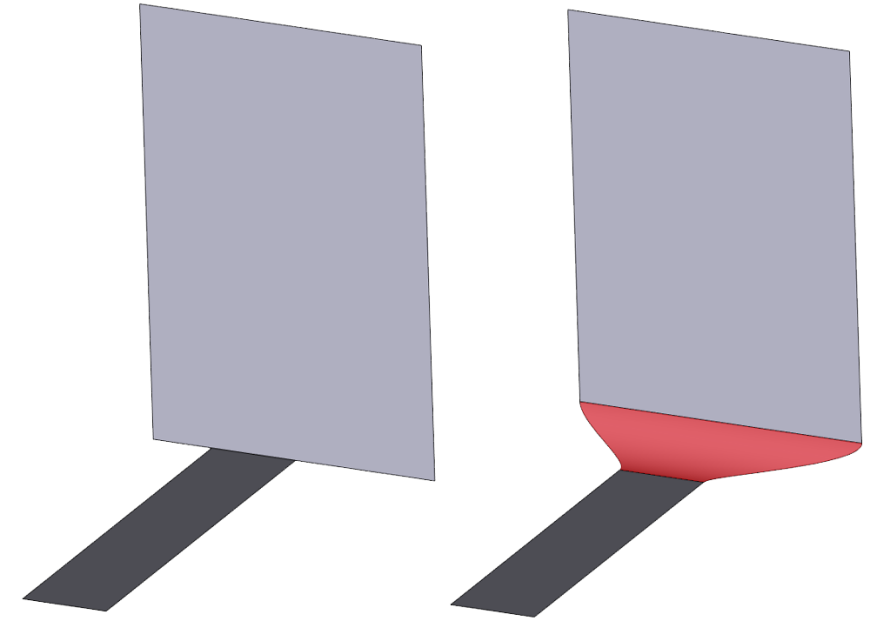Рис. 22. Сглаживание ребра поверхностного тела

В ядре RGK функциональность сглаживания граней и рёбер реализована, по сути, одним и тем же алгоритмом — отличие только в интерфейсе верхнего уровня, но при этом решаются классические задачи сглаживания граней (рис. 23-25).

Сглаживание граней, принадлежащих разным телам

Рис. 23. Сглаживание граней, принадлежащих разным телам

Сглаживание граней с удалением сложной топологии

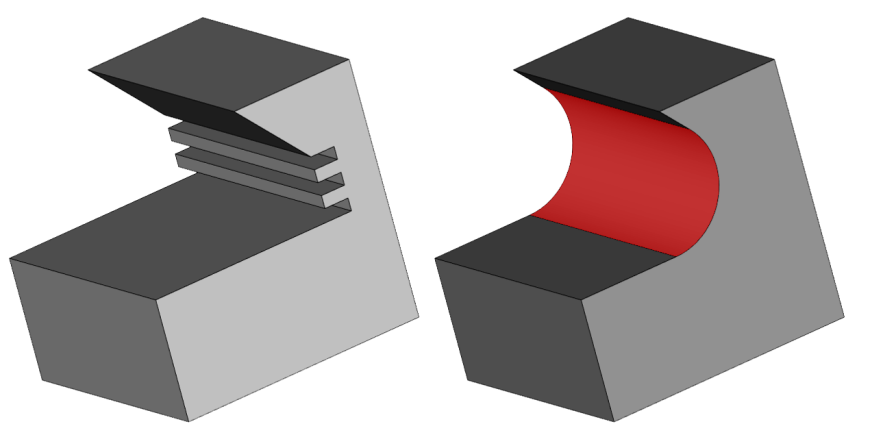Рис. 24. Сглаживание граней с удалением сложной топологии

Пример трёхгранного сглаживания — поверхность, касательная к трём стенкам

Рис. 25. Пример трёхгранного сглаживания — поверхность, касательная к трём стенкам

Продолжение в следующем материале.