Печатные пряники и Mathematica

В этой статье я хочу рассказать о методе создания моделей цилиндрических печатей для нужд подсобного хозяйства. Это может пригодиться как на кухне - делать забавные персональные печеньки, на стройплощадке - создавать уникальные или не очень декор штукатурки под различные материалы или оформлять обои, ткани повторяющимися рисунками. Словом, на что есть потребность. Для чего-же вообще была нужно цилиндрическая печать раньше?

Цилиндрическая печать — выточенный из различных материалов небольшой цилиндр с продольным осевым отверстием, который использовался в Древнем мире в качестве удостоверения личности автора документа или свидетеля его подписания. Боковая поверхность цилиндра содержала уникальную резьбу по камню. Наибольшее распространение цилиндрические печати получили в Месопотамии, где, начиная с шумерского периода, такая печать являлась важнейшим, всегда носимым с собой, атрибутом человека. Цилиндрические печати обычно изготавливались мастерами из твердого материала. Известны печати из аметиста, гематита, мыльного камня, известняка, обсидиана, нефрита, сердолика, карнеола, халцедона и других природных минералов. Большинство цилиндрических печатей изготавливались таким образом, чтобы после прокатывания по мягкому материалу получалось выпуклое изображение. Рисунки и орнаменты самой печати при этом делались вдавленными. Однако, некоторые цилиндрические печати, предназначенные в основном для других письменных материалов, сами изготавливались выпуклыми и использовались, например, для нанесения краски на документ из пергамента, или папируса.

Сразу должен оговориться, материал создан и адаптирован на русский язык на основе статьи George W. Hart - '3D-Printed Rollers for Making Escher-Cookies' .

Для создания моделей нам понадобится программный пакет Wolfram Mathematica. Пакет существует уже достаточно давно (в этом году 30 лет) и хорошо известен в среде профессионалов, но функциями поддержки 3D печати обзавелся относительно недавно.

Итак, для создания модели нам понадобится картинка, и программа, написанная на языке Wolfram Language. Скачать ее можно со страницы по ссылке выше. Ниже я привожу ее текст с комментариями работы.

SetDirectory[$UserDocumentsDirectory];

img = ColorConvert[Import[SystemDialogInput['FileOpen']], 'Grayscale'] (* загрузить файл с картинкой в градациях серого в диапазоне цветов 0..1 *)

height = 2.0; (* высота цилиндра, величина будет задаваться слайсером как мм или дюймы *)

alpha = 0.1; (* максимальный размер рельефа, в долях от высоты цилиндра, используйте отрицательное значения для инверсии *)

{n, m} = ImageDimensions[img];

rMid = n * height/(2 Pi m) ; (* средний диаметр*)

r = Map[rMid - alpha height (# - 0.5) &, ImageData[img], {2}]; (* пересчет в полярные координатах *)

xyz = Table[{r[[j, i]] Sin[2 Pi i/n], r[[j, i]] Cos[2 Pi i/n], (1 - j/m) height}, {i, 1, n}, {j, 1, m}]; (* конвертация в декартовы координаты *)

(* цилиндр состоит из трех частей - рельефной поверхности и круглых верха и низа *)

surface = Table[{xyz[[i, j]], xyz[[Mod[i + 1, n, 1], j]], xyz[[Mod[i + 1, n, 1], j + 1]], xyz[[i, j + 1]]}, {i, 1, n}, {j, 1, m - 1}];

bottom = Table[{{0, 0, 0}, xyz[[i, m]], xyz[[Mod[i + 1, n, 1], m]]}, {i, 1, n}];

top = Table[{{0, 0, (1 - 1/m) height}, xyz[[Mod[i + 1, n, 1], 1]], xyz[[i, 1]]}, {i, 1, n}];

g = Graphics3D[{EdgeForm[], Map[Polygon, Join[surface, top, bottom]]}] (* построение 3d модели *)

Export[SystemDialogInput['FileSave', 'roller.stl'], g] (* экспорт в файл *)

Эта программа выполняет математическое преобразование градаций серого с картинки в координаты, а затем выполняет операции преобразования систем координат. Изначально файл (полноценная картинка при импорте преобразуется в градации серого) с изображением представляется как таблица, которая кодирует величину почернения пиксела как функцию x и y координат на картинке. Программа преобразует x и y в угол и высоту в цилиндрической системе координат в полном диапазоне x, растянутым до одного полного оборота, при этом правая и левая стороны изображения объединяются. Радиус цилиндра выбирается так, чтобы отношение высоты цилиндра к длине окружности равнялось отношению высоте изображения к его ширине. Затем этот радиус изменяется в каждой точке путем добавления приращения соответствующего градации серого в соответствующем пикселе.

Параметр alpha, используется для масштабирования глубины рельефа. Большое значение alpha соответствует тому, что белые области изображения будут глубже утоплены в цилиндре, оставляя черный, чтобы выступать из цилиндра и делать более глубокие отступы в печенье. Задание alpha равное 0 на выходе создаст гладкий цилиндр без текстуры. Отрицательное значение параметра alpha меняет направление приращения, т.е. светлые области на изображения будут выступать из цилиндра.

Далее цилиндрические координаты преобразуются в трехмерные декартовы координаты. Сверху и снизу цилиндра добавляются круглые колпачки, для получения замкнутой модели. Затем модель экспортируются в STL файл

Рассмотрим на примере как это всё работает. Сначала ищем подходящую картинку. Например такую:

Далее приводим её к формату подходящего для модели. Из цветной в черно-белую программа преобразует сама, но нужно понимать пару моментов. В картинку не должно быть альфа-канала или прозрачных пикселов. Нужно подобрать разрешение картинки: высокое разрешение даст большой файл модели и будет долго обрабатываться, так что нужен компромисс. По моему опыту размер 500-800 пикселов по одной стороне дает вполне хорошие результаты. Далее при полноцветной картинке нужно чтобы цвет пиксела не сильно отличался от соседей, иначе будет шумно. Поэтому лучше всего картинку переделать в каком-нибудь редакторе, убрать резкие переходы от светлого к темному. Это лучше всего сделать, пройдясь фильтром Blur. Я пользовался Gausian blur с размером 2 пиксела. В итоге получилась такая картинка:

Скармливаем её программе и получаем модель. Модель можно покрутить, увеличить или уменьшить, поиграться с параметром alpha, его величиной и знаком.

После этого делаем экспорт в .STL файл. Отправляем на печать и прокатав по кусочку теста получием примерно вот такой результат.

Еще пример. Слева исходная картинка, справа обработанная, на основе которой создавалась модель.

Результат на тесте. Финальная картинка получилась не контрастная, поэтому результат тоже не очень. Кроме того, надо было бы сделать инверсию, тогда было бы лучше видно Ракету, но хуже надпись.

Это, с моей точки зрения, самая удачная модель. Снова сверху оригинал картинки. Ниже обработанная, на основе которой создана печать.

Результат работы на тесте,

Это отпечаток модели Эшеровской картинки созданный автором методики. Авторские модели можно скачать со страницы указанной в начале статьи, я напечатал только одну из предложеных.Это все использованные печати.

Ссылки на модели:

Роллер 'Пошалим' - http://3dtoday.ru/3d-models/for-home/kitchen/rolik_dlya_pechenya_poshalim/ Роллер 'Vault boy' - https://www.thingiverse.com/thing:3113926 Роллер 'San Andrés' - https://www.thingiverse.com/thing:3103580

Эшеровские всадники - http://georgehart.com/rollers/

Что еще можно сделать?

Например, легко и просто получаются валики для структурной штукатурки, их сейчас в большом количестве можно найти в интернете.

Например, такие:Что для этого нужно? Берем паттерны узоров Переводим их в модель цилиндрической печати, распечатываем и пользуемся. Правда для удобства ещё придется смоделировать ручку. Но для посетителей этого сайта это точно не проблема.

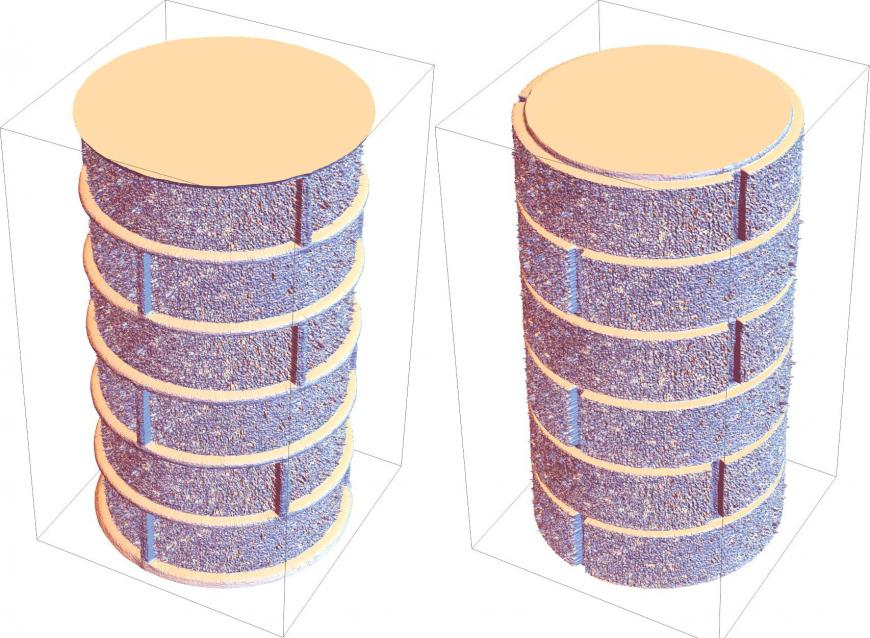
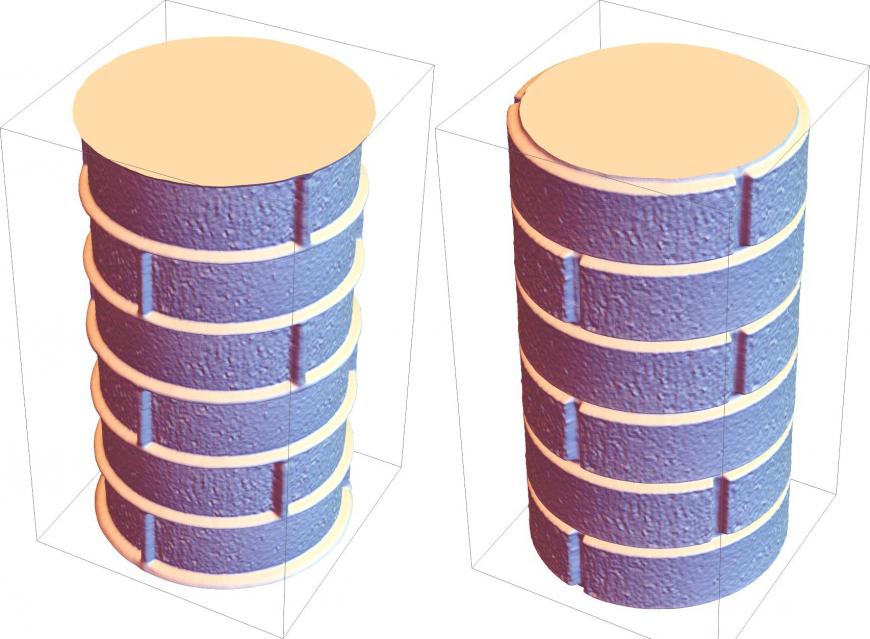
В качестве бонуса, не печеньки. Давайте сделаем печать для имитации кирпичной кладки.

Ищем подходящую картинку. Здесь я не заботился о том, чтобы кирпичи были одинаковой длины. Из-за того, что правый край соединится с левыми в модели в нечетных кирпичах будет очень большой кирпич, а в четный очень маленький.Обрабатываем как было описано выше. Gausian blur, 2 пикселаПропускаем через программу.Это два варианта с одной и той же исходной картинкой, где параметр alpha положительный и отрицательный. Очень хорошо виден цифровой шум.А это тоже самое, но уже с обработанной картинкой в качестве исходника. Шум гораздо меньше.Выбираем понравившийся вариант. В общем этот простой скрипт открывает большое поле для экспериментов, где каждый сможет сделать что-то полезное для себя.

В этой статье даже и не начинал рассматривать всех возможностей Wolfram Mathematica. Из всего многообразия был использован только экспорт в STL. Очень многое осталось за рамками этой статьи. Если будет интерес к этой теме, то можно будет рассмотреть и другие особенности, и возможности этого пакета.