Определение кривизны плоских кривых

Захотелось улучшить точность создания моделей в Blender, для чего решил соорудить устройство измеряющее радиус кривизны. Мне нужно было измерить конкретную выпуклую кривую. Подумал про аналоги сферометра, но для плоскости это слишком сложно, нам бы чего попроще.

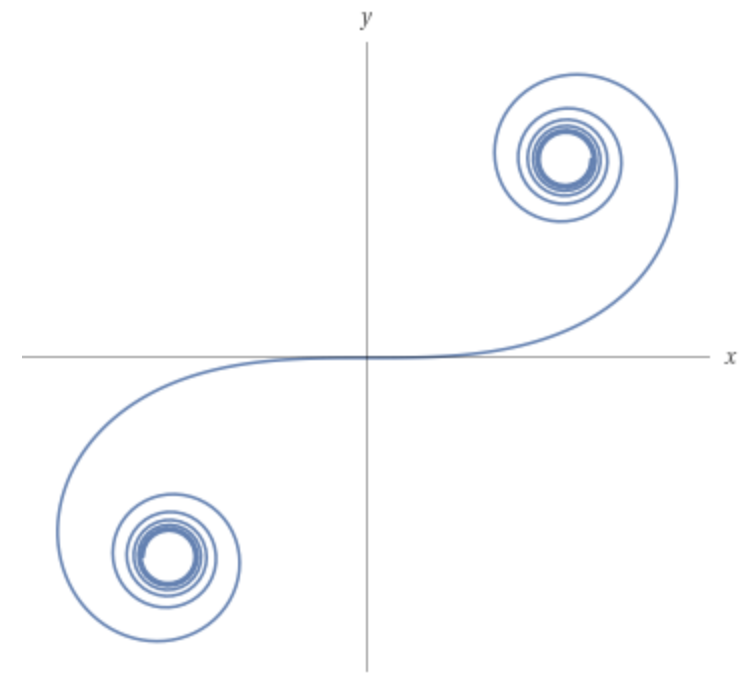
Немного повспоминав математику и погуглив википедию, дошел до мысли, что вот можно соорудить лекало по кривой Эйлера - у неё кривизна линейно зависит от её собственной длины. Вот так выглядит эта кривая:

Чуть было не собрался печатать, но тут подумал, что есть два аспекта:

- во-первых, ну допустим, я приложил лекало к детали и нашел точку совпадения кривизны. Как я буду дальше действовать? отмечу точку карандашиком и пойду за ниточкой, измерять длину кривой? Это как-то не очень удобно.

- во-вторых, и в главных, даже если я нанесу разметку, те кривизны, которые меня интересуют (допустим от 10см до метра) все сосредоточены в начале кривой, и как следствие, детализация там уменьшается. Точка "кривизна 40см" и "кривизна 50см" будут непозволительно близко.

Нужно что-то попроще. Ну мы всё-таки живем в 21 веке, и я решил подобрать кривую, кривизна которой будет линейно зависеть от x.  Тогда я просто размечу деления на линейке равномерно, и это будет соответствовать той точке, в которой приложенная линейка с деталькой совпадет.

Отлично. Дальше я вооружился чатом гпт в помощь и соорудил следующее. Сначала попробовал "в лоб" решить диф.ур, так чтобы радиус кривизны R(x) линейно зависит от x. не получилось, понял, что сложно. Попытка подобрать кубический полином тоже провалилась.

Ага, подумал я! давайте попробуем методом Рунге-Кутта! начнем с точки (1,0) и будем последовательно приращивать кривую, так чтобы её вторая производная удовлетворяла тому чему надо. Не тут-то было... вычисление "быстро взорвалось", очень близко от старта первая и вторая производная улетали в космос, чтобы компенсировать друг друга. Беда.

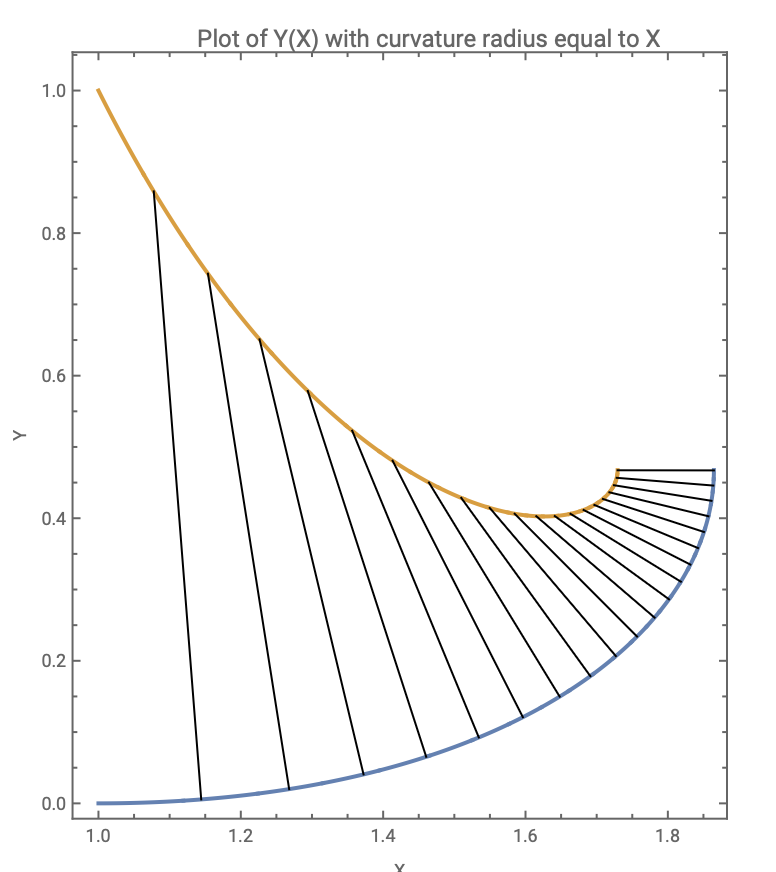
Немного почесав в голове, понял что параметризовать кривую надо не по оси X, а вдоль самой себя, то есть, по длине. Ура. Эту модификацию я сделал сам - без помощи искуственного интеллекта. Небольшой скрипт в бесплатнодоступном wolframcloud нагенерил мне вот это. Похоже, да?

(тут нас синяя кривая интересует) До боли знакомая линейка из детства.

Дальше возникли следующие затруднения. Ок, допустим я её распечатаю. Но самый большой радиус кривизны, который она сможет измерить (соответствует единице) будет равен её размерам. То есть, чтобы измерить что-то с радиусом кривизны 45 см, мне нужна линейка величиной 45см и больше. Опять беда.

Ну, вобщем, не буду томить, подкрутил уравнение так, чтобы при шаге по оси x на дельта x, радиус кривизны уменьшался на 5 дельта x.  То есть, линейка с масштабом кривизны 1:5.

Дальше - дело техники, попросил чатгпт перенести получившийся массив чисел в blender. Он подсказал мне, как сконвертировать скрипт в питон, и сгенерировать там меш. Это довольно мило. В итоге, повозившись с моделью, получил вот такую линейку:

Могу поделиться моделями линеек в масштабе x1 и x5