Фрактал Чезаро ауксетик?

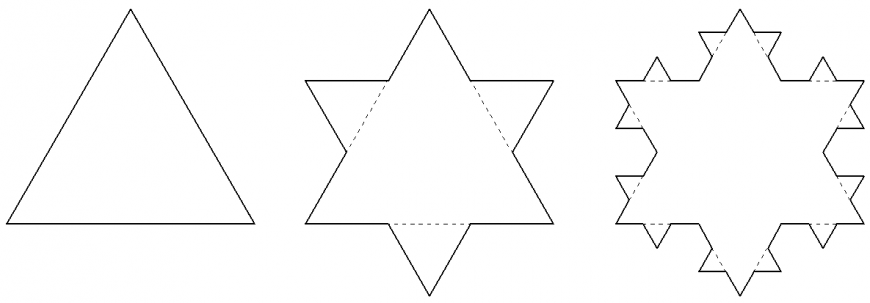
Просматривая схемы различных фракталов, я обратил внимание на снежинку Коха, а точнее на ее частный случай – фрактал Чезаро (Cesaro). Глядя на него, я предположил, что из него можно получить ауксетик. Подробнее о том что такое ауксетики я рассказывал тут. Для начала вспомним или узнаем (для кого что актуальнее) что такое снежинка Коха. Она строится на сторонах равностороннего треугольника. На рисунке показан исходный треугольник и две первые итерации. Тонким пунктиром показано то, что удаляется на данной итерации.

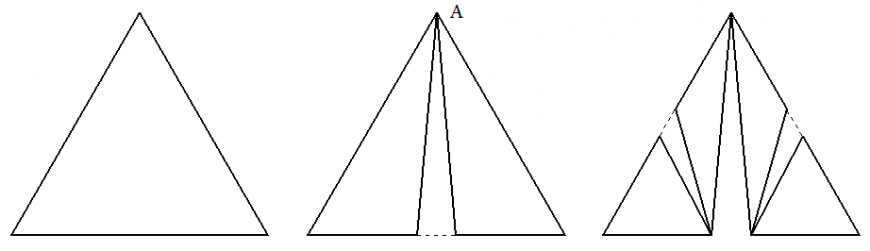
Фрактал Чезаро отличается следующим: Мы не добавляем треугольники, а наоборот вырезаем треугольные области из исходного. И делаем это не на всех сторонах треугольника, а только на одной. Чтобы было понятно вот рисунок исходного треугольника и первые две итерации.

Из исходного треугольника на первой итерации мы вырезали область в виде равнобедренного треугольника, при этом в вершине А линии двух треугольников сходятся вместе. Как итог первой итерации получили два новых треугольника. Затем, на следующей итерации, в каждом из этих треугольников мы таким же образом вырезаем область. Далее процесс можно повторять до бесконечности.

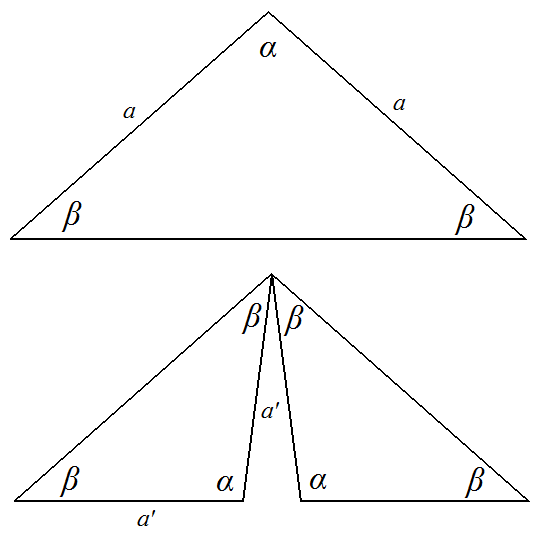
Если взять за исходный не равносторонний треугольник, а равнобедренный и при этом с длиной сторон меньше длины основания, то можно получить фрактал Чезаро, у которого на каждой итерации будут получаться опять равносторонние треугольники с углами, равными углам исходного. Покажем это на рисунке.

Исходный треугольник имеет длины сторон, равные а и углы α и β (как мы помним, в равнобедренном треугольнике углы при основании равны). Так вот, в соответствии с фрактальным делением Коха мы можем разделить этот треугольник на два новых, так, что они окажутся подобными исходному. Здесь вспоминаем условия подобия треугольников из школьного курса геометрии))). У новых треугольников все углы равны соответствующим углам исходного треугольника, а длины сторон пропорциональны соответствующим длинам исходного треугольника.

Увидев именно такой вариант фрактала Чезаро, я предположил, что на его основе можно смоделировать ауксетик. Напомню, что ауксетик – это материал с отрицательным коэффициентом Пуассона.

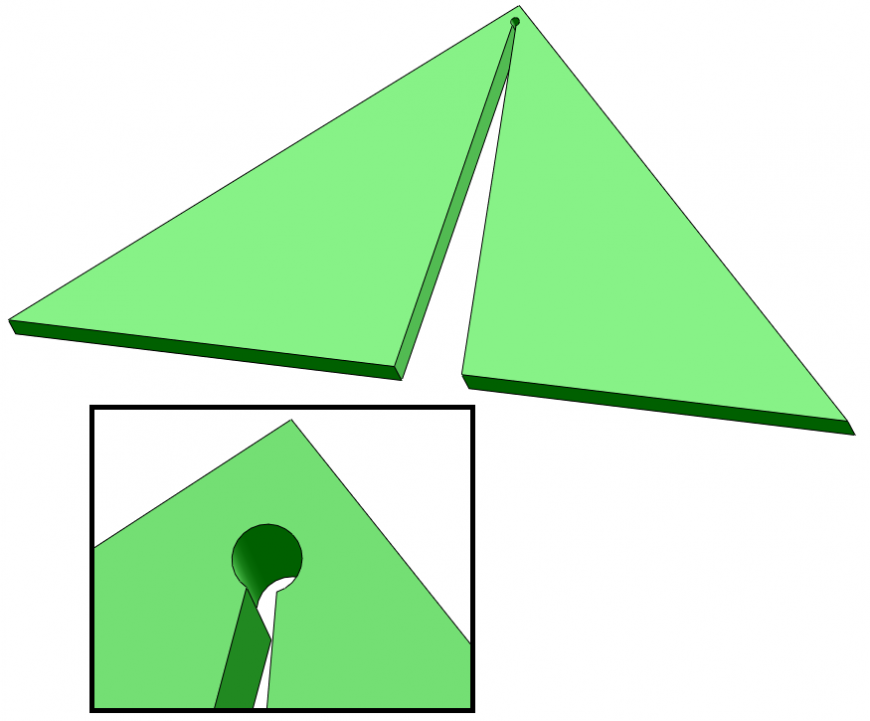
Смоделировал и распечатал несколько итераций. При моделировании учитывал, что получаемые треугольники соединятся только в одной точке, и, чтобы распечатанная модель не развалилась, доработал места соединений. Печатал флексом.

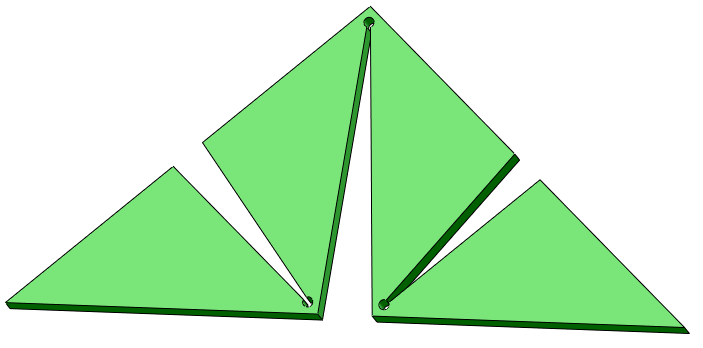
Первая итерация:

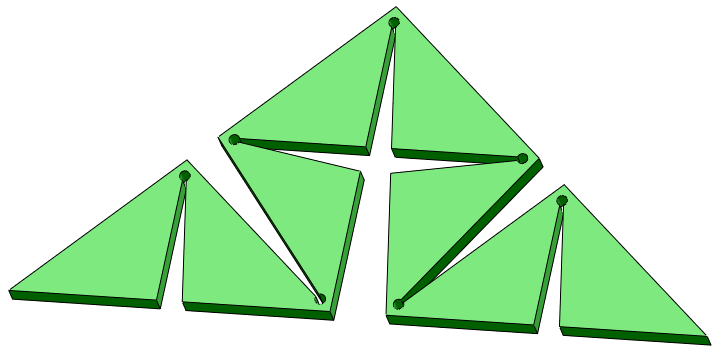
Вторая итерация:

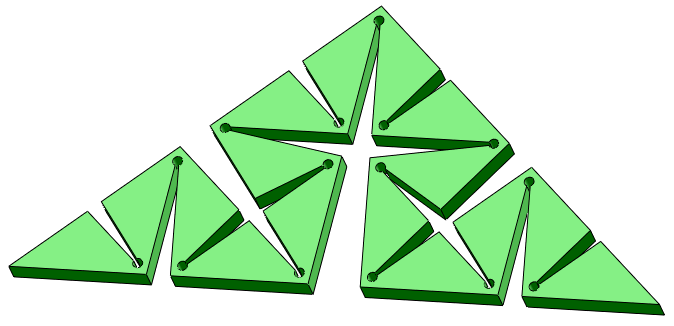
Третья итерация:

И последняя – четвертая итерация:

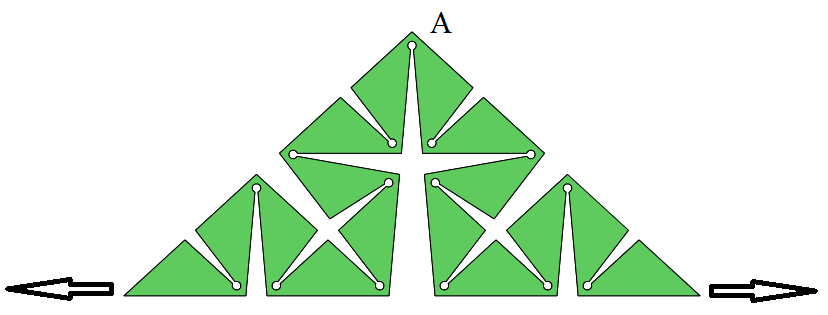
Далее проверка моего предположения. Методика проверки показана на рисунке. При растяжении вдоль направления стрелок вершина А должна будет переместиться вверх. Если это произойдет, то мое предположение будет верным.

Первая итерация: при растяжении точка А движется вниз, следовательно коэффициент Пуассона положительный. Предположение не верно.

Вторая итерация: При растяжении сначала точка А остается неподвижной, затем начинает двигаться вниз. Таким образом, здесь можно наблюдать переменную величину коэффициента Пуассона – от нулевого значения до некоторой положительной величины.

Третья итерация: При растяжении точка А сначала движется вверх, а значит значение коэффициента Пуассона отрицательное! Затем, при дальнейшем растяжении, точка А начинает опускаться.

Четвертая итерация: Здесь наблюдается ситуация, аналогичная третьей итерации. При этом движение точки А вверх более заметное.

Мое предположение оказалось верным: на основе фрактала Чезаро можно сделать ауксетик, начиная с третьей итерации. Если быть более точным, то можно получить не только ауксетик, а, даже, материал с переменным коэффициентом Пуассона – все будет зависеть от диапазона деформаций.

Отмечу, что я проверил только принципиальную возможность этого. Для определения точных величин коэффициента Пуассона нужно специальное оборудование и более качественные образцы. Тогда можно проследить как меняется коэффициент Пуассона с ростом итераций и какие принимает значения при растяжении каждой итерации в отдельности.