Ауксетики. Складывающиеся схемы.

В предыдущей статье, посвященной ауксетикам, я рассказывал что это такое и приводил несколько схем. В этой статье речь пойдет о схемах ауксетиков, способных складываться в монолитную структуру, то есть в сложенном состоянии структура не имеет сквозных отверстий. Все схемы, описанные ниже, можно разделить на два вида: первый вид сохраняет монолитную структуру только под действием внешней силы; второй – сохраняет монолитную структуру даже после снятия внешний нагрузок.

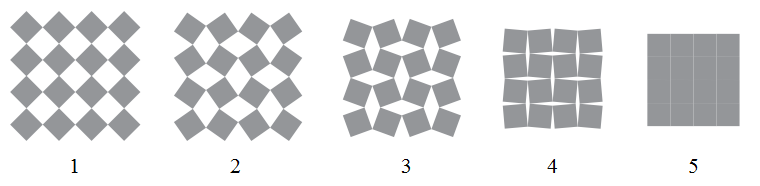
Самым простым примером первого вида будет схема [1], изображенная на рисунке:

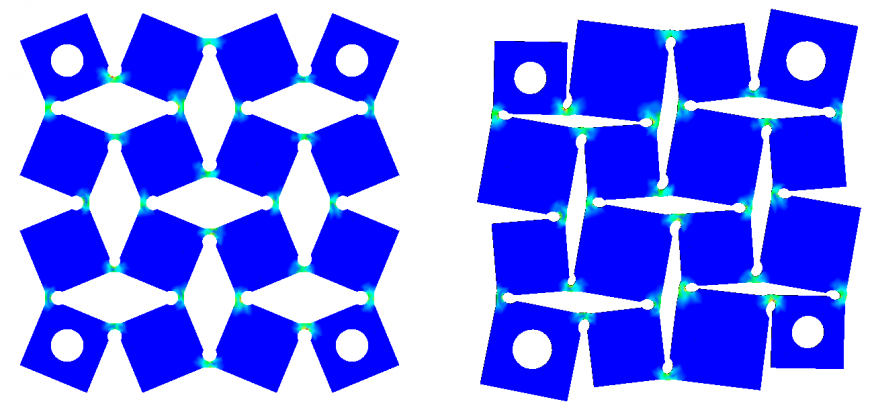
Схема представляет собой набор квадратов, соединенных по углам. Напечатанная одной деталью, эта схема кинематически эквивалентна набору шарнирно соединенных квадратов. В этот раз дополнительно решил проанализировать схемы с помощью метода конечных элементов. Расчеты делал в бесплатной программе Z88Aurora. Результаты показаны на рисунке:

Изображено состояние до деформации и после. Решалась линейная задача, поэтому величины деформации и нагрузки не привожу, в этом нет смысла – они условные. Для меня было интересно получить качественный результат.

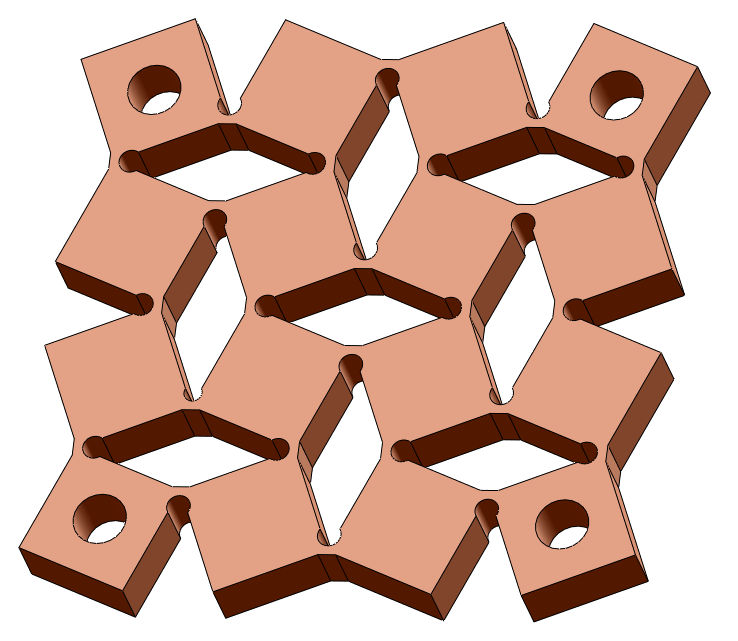
Переходим к материализации схемы. Как правило, под 3D-печать схемы приходится дорабатывать. По созданной модели видно, что места соединения квадратов были доработаны для того, чтобы схема нормально складывалась.

В конце статьи есть видео, на нем можно увидеть анимацию деформирования (складывания) этой и других конечно-элементных моделей, а также складывание всех напечатанных на 3D-принтере схем.

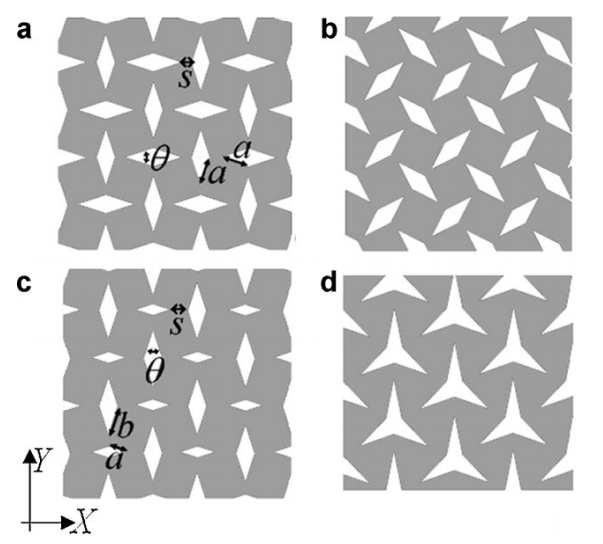
Переходим ко второй схеме [2]. Эта схема похожа на первую. Общий вид показан на рисунке (вид d):

Эта иллюстрация приведена прямо из статьи [2] и на ней есть первая схема, но здесь отличаются подходы к созданию таких схем. Идея авторов состоит в том, что они создают ауксетики с помощью простой перфорации листового материала. Обратите внимание, схемы можно получить вырезая сравнительно простые регулярные элементы (в частности ромбы). А можно получить ауксетик вообще просто делая надрезы на листовом материале:

Возвращаемся ко второй схеме:

Результаты конечно-элементного анализа:

Для этой схемы деформации видны уже не так наглядно. При этом напечатанная модель складывается именно так как нужно – зазоров между треугольниками не остается.

А на очереди схемы поинтереснее. Следующая схема [3] показана на рисунке:

При сжатии такой схемы шестиугольники поворачиваются относительно друг друга, прижимая к себе «лепестки». Отмечу, что в статье [3] авторы предлагают такую схему как один из вариантов складывающихся конструкций для корпусов космических аппаратов. Схема интересна тем, что ее можно одинаково хорошо сжимать в любом направлении.

Результат конечно-элементного анализа:

Все выше описанные схемы возвращают свою первоначальную форму после снятия нагрузки. Теперь же рассмотрим несколько схем, которые имеют две устойчивые формы своей структуры. Это так называемые бистабильные схемы.

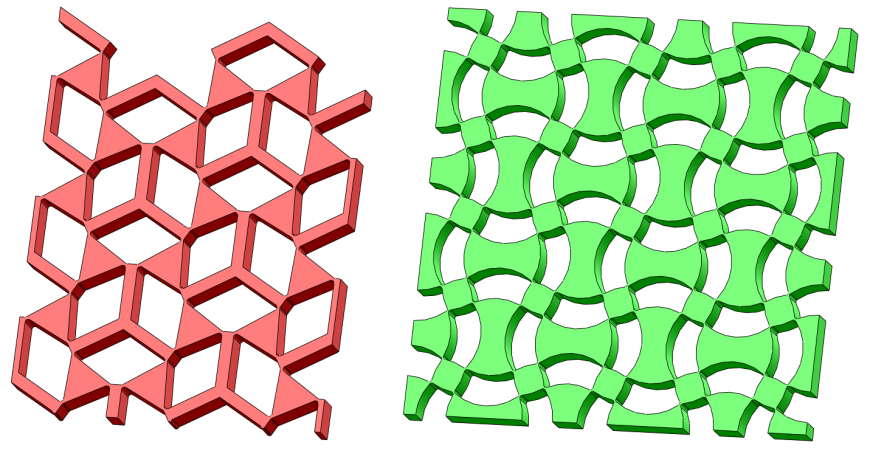
Для начала рассмотрим сразу две схемы такого вида [4]:

При создании этих схем авторы научной статьи вдохновлялись средневековыми орнаментами:

Орнаменты нанесены на две Башни Харракана (Kharraqan towers) в Иране. Первая башня была построена в 1067 году, а вторая в 1093 году.

Делаем модели, адаптированные для печати:

И результат в двух положениях:

Еще одна схема с двумя равновесными формами [5]:

Ее конечно-элементная модель:

У этой схемы выяснилась одна интересная особенность. Точнее, это свойственно именно тому варианту схемы, который получился у меня. В сложенном состоянии она удерживается сама только тогда, когда сложены все ее элементы. Вот два стабильных положения:

Для данной схемы можно отметить наличие относительно больших зазоров. Я напечатал несколько различных вариантов и получить монолитную структуру мне удалось на них только если дополнительно сжимать сложенную схему.

В завершении видео, на котором можно увидеть как именно складываются все рассмотренные структуры, движение их кинематических схем, а также анимацию деформирования конечно-элементной модели.

На этом пока все.

Источники:

1. Coulais C., Sabbadini A., Vink F., van Hecke M. Multi-step self-guided pathways for shape-changing metamaterials. Nature, –2018 –V.561(7724), –p.512–515.

2. Grima J. N., Gatt R. Perforated Sheets Exhibiting Negative Poisson’s Ratios. Advanced Engineering Materials, –2010 –V.12(6), –p.460–464. 

3. Hanaor A., Levy R. Evaluation of Deployable Structures for Space Enclosures. International Journal of Space Structures, –2001 –V.16(4), –p.211–229. 

4. Rafsanjani A., Pasini D. Bistable auxetic mechanical metamaterials inspired by ancient geometric motifs. Extreme Mechanics Letters, –2016 –V.9, –p.291–296. 

5. Haghpanah B., Salari-Sharif L., Pourrajab P., Hopkins J., Valdevit L. Multistable Shape-Reconfigurable Architected Materials. Advanced Materials, –2016 –V.28(36), –p.7915–7920.